原因としてはいくつかありますが、ピアノ線においては剛性が非常に高いので振動の節になる部分が影響を受けて波長が短く(振動数が高く)なるためと言われています。
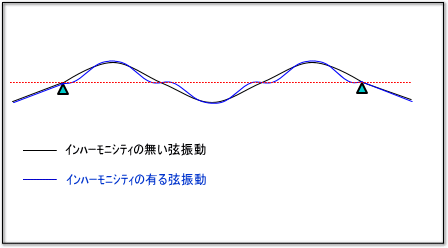 |
左図のように、インハーモニシティの有る弦は波長の節となる部分が高剛性のため、きれいな曲線を描かず結果的に短い波長になってしまいます。 ピアノにおいては張力(テンション)や弦の剛性によって起きる訳ですが、厳密には設計通りに正確に1台1台組み立てられているわけではないのでインハーモニシティの出方はピアノそれぞれ固有の出方をします。 ピアノの調律が器械(チューナー)を使ってできない理由がそこにあるわけです。一般的に弦長が短く、テンションが高いピアノ(小型ピアノ)ほど、このインハーモニシティのズレは大きくなります。 奥行き3メートル近いコンサートグランドピアノであってもインハーモニシティは存在します。 |
実際のピアノで(YAMAHA U3) 49A(440Hz 弦長412mm
ピアノ線直径0.975mm)の弦のインハーモニシティ
を求めてみましょう。
インハーモニシティを計算する公式は以下の公式(アル・アンダーソン博士)を使いました。
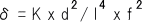
δ=インハーモニシティ値 K = 係数(3.3 x 10 の 15乗) d =弦 直径 l = 弦長 f = 振動数
δ= (3.3*(10^15)x(0.975^2))/((412^4)x440^2)
δ= 0.562379
そして、1オクターブ上の61A(計算上880Hz)と同じ2倍音の振動数をインハーモニシティを含めて計算すると以下のようになります。
T = P x P x I
P = 倍音次数(2倍音なら2) I = インハーモニシティ値 T = 倍音におけるインハーモニシティ値 (単位:cent)T = 2 x 2 x 0.562379
T = 2.249516(cent)
従ってこの場合、61Aと同じ音程の2倍音は約2.25セント高いことが解ります。
ハンマーは打弦後、反動と重力によって落下します。落下後はバックチェックによってキャッチされ、次の打弦のためにジャックがシャンクローラーの下にスムーズに戻るのを待ちます。これをハンマーと鍵盤の関係で表しますと以下の図のようになります。
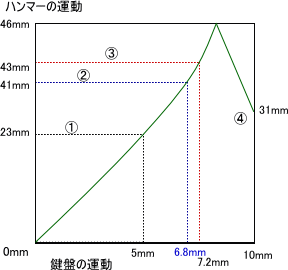
②鍵盤が6.8mm沈んだところでドロップスクリューにレペティションレバーがあたって運動が止まる。小ジャックがレギュレティングボタンにあたって運動が止まる。以上の動作は同時であることが望ましい。
何故ならばハンマーに伝わる力にロスが生じるからである。
③鍵盤が7.2mm沈んだところでジャックがローラーから抜けて打弦する。
③'鍵盤が7.5mm沈んだところでハンマーが弦を打つ。
④鍵盤が10mm沈んだところで鍵盤の運動が止まる。ハンマーがバックチェックにくわえられ運動が止まる。以上の動作は動じであることが望ましい。
何故ならば同時でなければ鍵盤運動終了前後にバックチェックにハンマーがくわえられた衝撃を感じるからである。
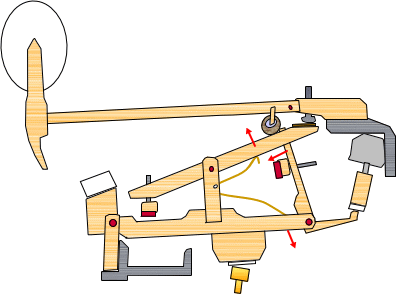 |
①レペティションレバーはスプリングの力によって上に上がる。
②ジャックはスプリングの力によって引き戻される。 アップライトはこの機構が無いので、鍵盤が次の打鍵の位置に戻るまでジャックはハンマーを持ち上げることができない。 |
