I = 慣性モーメント m = 質量 r = 半径
m(質量)をバランスピンから鍵盤先端までの重さ、r(半径)をバランスキーピンから鍵盤先端までの距離とします。仮にmを 100g、rを30㎝とすると以下の公式が成り立ちます。
I = 100 x 30^2 = 100 x 30 x 30 = 90000 になります。しかし、ピアノの場合はバランスキーピンを支点として鍵盤側とアクション側で 55 ~ 58 gでつりあうように設計されています。それを公式で表すと以下のようになります。
I = 慣性モーメント m1 = 鍵盤側質量 r1 = 鍵盤側半径 m2 = アクション側質量 r2 = アクション側半径
グランドピアノとアップライトピアノを比較すると、鍵盤の長さとアクションの重量がグランドピアノのほうが大きいのは当然です。従って静的同等質量(静止した状態)が55g であっても動的同等質量(鍵盤を動かした状態)では距離の二乗大きくなるのです。
例) アップライトピアノ
m1 = 100g r1 = 200㎝ とした場合、55g の質量で鍵盤がつり合うなら r2 = 133.3㎝ なので m2 は(100 + 55) x 200 = m2 x 133.3
m2 = 232.5581g
例) グランドピアノ
m1 = 200g r1 = 400㎝ とした場合、55g の質量で鍵盤がつり合うなら r2 = 200㎝ なので m2 は(200 + 55) x 400 = m2 x 200
m2 = 510g
になります。これが鍵盤を押した場合は慣性モーメントの計算で
例) アップライトピアノ打鍵時
I1 = 155 x 200^2
I1 = 6,200,000
例) グランドピアノ打鍵時
I2 = 255 x 400^2
I2 = 40,800,000
如何にグランドピアノのタッチが重いかお分かりになるでしょう。
*実際は運動角度や重心の関係で上記の計算通りにはなりません。
ハンマーは打弦後、打弦点から15ミリのところでバックチェックによってキャッチされ、次の打弦のためにジャックがシャンクローラーの下にスムーズに戻るのを待ちます。
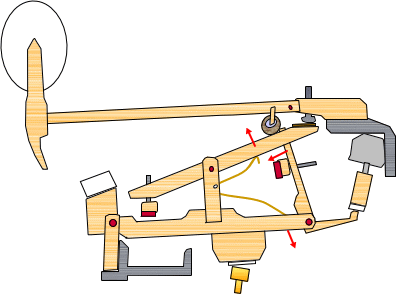 |
①レペティションレバーはスプリングの力によって上に上がる。
②ジャックはスプリングの力によって引き戻される。 アップライトはこの機構が無いので、鍵盤が次の打鍵の位置に戻るまでジャックはハンマーを持ち上げることができない。 |
ではアップライトはどうでしょう。
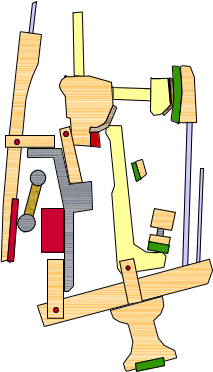 |
①鍵盤をわずかに戻すと、キャッチャーがバックチェックから離れる。
②ジャックはスプリングの力によってウィペンに対して垂直になろうとし、始動位置に戻ろうとする。 ③鍵盤が5ミリ戻るとその上に乗るウィペン、ジャック、バットが下がる。ダンパーが止音する。 ④ハンマーはバットの形状から、ジャックがバットを動かすことができる位置にないと打弦することができない。 以上のことから、グランドアクションはアップライトアクションと比較して打鍵後約1ミリ戻るだけで次の打鍵が行えるので、トリル・トレモロが高速に行えます。そしてトリルしながらのクレッシェンド・デクレッシェンドも行えます。また、打弦距離が短い状態での発音も可能なので発音のレンジも広いのです。 |